While nodal network statistics focus on an individual node, structural network statistics analyze the network as a whole. This analysis is essential to understanding the behavior of a network as a whole. While many statistics may be calculated, the most commonly used are network density, clustering coefficients, centralization indices, and descriptive statistics.

Network Density

Network density is a measure of the number of connections in a network divided by the total number of connections possible. This is calculated as 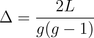for an undirected network when L is the number of lines in the network and g is the number of nodes in the network. A network with high density will be more connected than one with low density.

Clustering Coefficients

Clustering coefficients measure how tightly knit a community is. In an undirected graph, the clustering coefficient of a node is calculated as 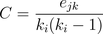, in which e_jk total number of connections between the neighbors of node i, and k_i is the degree of node i. A clustering coefficient of one signifies that all neighbors of a given node are connected to each other, while a value of zero means no neighbors are connected to each other, and a value in between shows that some, but not all, neighbors are connected. Therefore, higher clustering coefficients signify higher interconnectedness within a local community.

Centralization Indices

Centralization indices are aggregations of nodal network statistics. A centralization index approaching 1 indicates large variability in the nodal statistic, while a centralization index approaching zero indicates little to no variability. A centralization index is calculated for any nodal network statistic as 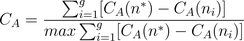, and can be calculated based upon any nodal network statistic.

Descriptive Statistics

Descriptive statistics account for the averages and variations of nodal network statistics. The average of a any nodal network statistic is calculated as 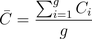. As an example, a high average proximity centrality suggests that there is a high level connectedness within an entire network. The variation of a nodal network statistics is calculated as 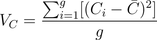. This measure, like centralization indices, quantifies the variation of a particular nodal statistic between different nodes in a network.