Network analysis uses the statistic centrality to study the interactions between individuals in a network. But quantitatively and theoretically, what does centrality mean?

Centrality is a statistic that allows for the meaningful differentiation of individual node by assigning values to them based upon their importance in a network. There are several different measures of centrality, and the meaning of each of these statistics changes with the types of connections used. Thus, the choice of appropriate centrality measure depends on the type of connection employed and information sought. Degree, proximity, prestige, and betweenness centrality are four common centrality measures.

Degree Centrality

Degree centrality is a measure of the aggregate degree of each individual node’s connection in a network to distinguish highly connected nodes from less connected ones. In this case, the degree of a node refers to the number of nodes to which a given node is connected. In other cases, such as those pertaining to directed graphs, the degree measure is referred to as indegree and, as the name suggests, only refers to the number of connections going into a given node.

Proximity Centrality

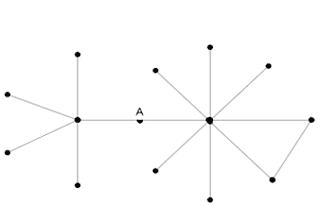
Proximity centrality is a statistic that attaches numbers to individual nodes by calculating the number of connections that separate a given node from all other nodes. This number is then divided by the total number of nodes, or input domain, to which that node is connected. The equation for this statistical node is 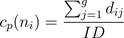, where n_i is the given node, and d_ij is the distance to another node. One can compare these numbers across nodes to evaluate position relative to other individuals in the network. Proximity prestige is particularly informative in star-like networks. As you can see in Figure 1, node A will register as being the most central node and the nodes that radiate out from node A will be less central as each connection increases the distance from the center.

Although proximity centrality can be useful in many ways, it does not take into account the positions of the nodes to which the original node attaches, nor does it account for the weights on the arcs or edges. In order to do this, prestige centrality must be used.

Prestige Centrality

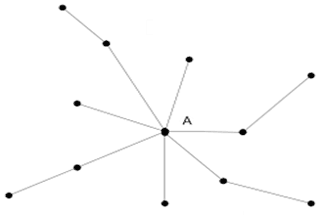
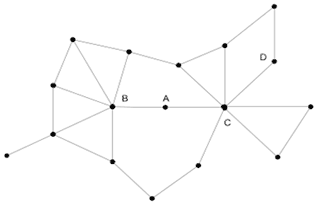
Prestige centrality accounts for the position of nodes to which an original node is attached. It also accounts for the weights on the arcs and edges of a network. In many cases, it is not just important what connections a node has, but it is also important what connections the nodes that it is connected to have. In Figure 2, when determining whether node A is more or less important than node D, it is evident that both nodes have two connections. However, it is node A that has the position of greater structural importance because it is connected to nodes B and C, the two most connected nodes in the network.

Prestige centrality measures account for this difference using eigenvector analysis. The most prevalent of which is Bonacich eigenvector centrality, calculated through the equation 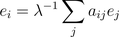. In the equation, the prestige of node i, e_i, is based upon the prestige of all nodes to which it attaches, e_j. Thus, in this case, the importance of a node is a function of the importance of the nodes to which the original node is connected.

It is important to note that, although Bonacich eigenvector centrality may be the most common weighted measure of centrality, it has been shown to be the most unstable statistic for gauging centrality. While prestige and proximity centrality account for a particular type of centrality that is about the frequency and intensity of connections, there are other conceptualizations of centrality that account for the necessity of flow between nodes or communities of nodes. The most common of these is betweenness centrality.

Betweenness Centrality

Betweenness centrality accounts for the necessity of flow between nodes and communities of nodes by measuring the importance of a bridge node in facilitating contact or interaction between other nodes in a network. Figure 3 demonstrates that although node A is not connected to many different nodes, it lies at a position of structural importance because node A is the only connection between the nodes of two separate communities.

The equation for betweeness centrality is 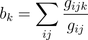, in which b measures the sum of the proportion of geodesic paths between every node that pass through a given node (g_ijk) and the total number of geodesic paths that exist in the network (g_ij).